3.结果与讨论
3.1.光密度生长曲线
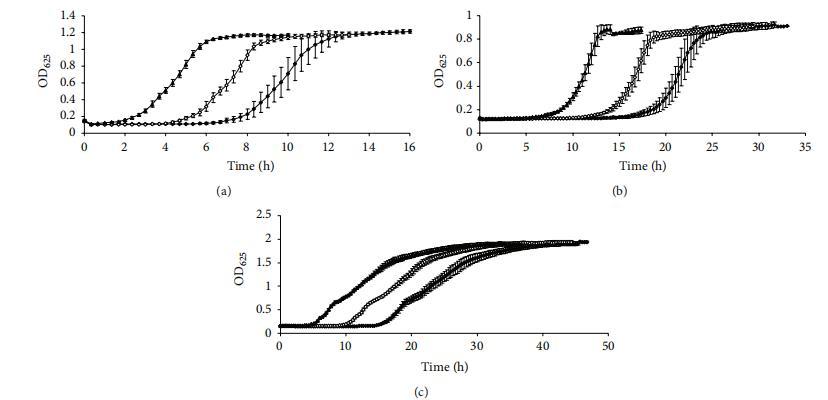
图1显示了蜡样芽孢杆菌INRA-AVTZ 415在30°C BHI中(a)、单核细胞增生李斯特菌CECT 4031在37°C TSB+YE中(b)和大肠杆菌CECT 515在37°C pH 5 TSB+YE中(c)以10²,10⁴和10⁶CFU mL⁻¹初始浓度开始的光密度生长曲线,绘制了每个采样时间的平均OD值。这些平均生长曲线各对应25-30条个体生长曲线。对应于一种微生物的所有生长曲线在指数生长阶段的斜率是平行的;即,生长率应相似,因为它们应代表相同微生物在完全相同的条件下生长的不同培养物。然而,随着初始浓度的增加,观察到延迟期持续时间逐渐减少。这种延迟时间的减少可以很容易解释,因为培养物花费更少时间达到吸光度增加的浓度。实际上,一些作者最近使用简单方程从OD测量推导真实延迟时间,并提供了微生物的初始浓度和观察到的延迟时间[24-26]。获得的相对较低的标准偏差值,特别是对于以10⁴和10⁶开始的生长曲线,表明生长曲线的可重复性。可以注意到,随着初始浓度的降低,误差条更大,这是由于小种群细胞间变异性增加的结果[2]。
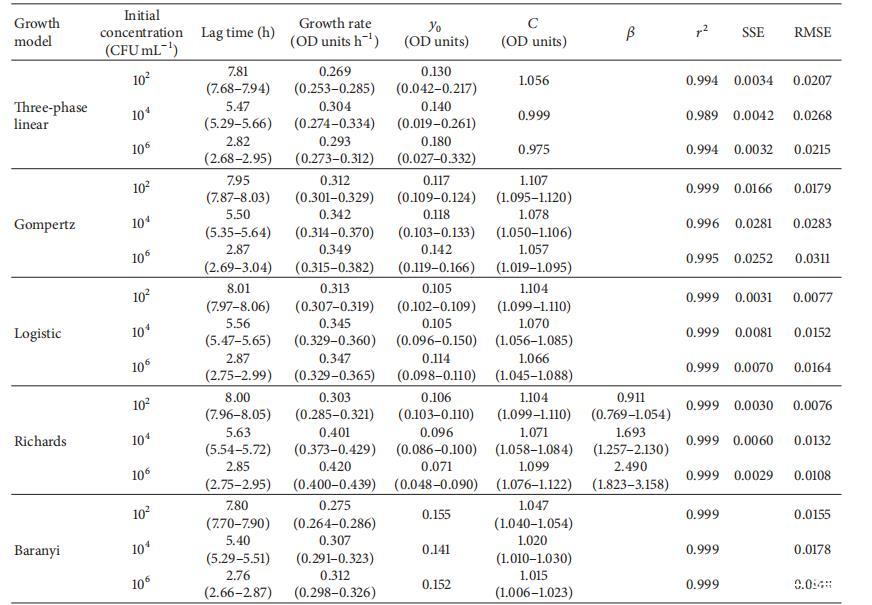
表2显示了三相线性、Gompertz、logistic、Richards和Baranyi模型对图1(a)所示蜡样芽孢杆菌平均OD生长曲线提供的生长参数。所有测试的模型都提供了这种微生物三种选定生长曲线预期的生长参数值。图1(a)显示蜡样芽孢杆菌的所有三条平均生长曲线在指数生长阶段大致平行。尽管以10⁶CFU mL⁻¹开始的曲线斜率略低,但只有logistic和Richards模型显示该曲线与以较高初始浓度开始的其他两条蜡样芽孢杆菌曲线之间存在显著差异(表2)。当比较不同模型给出的生长率值时,三相线性模型给出最低值(0.27-0.30 OD单位h⁻¹),其次是Baranyi模型(0.28-0.31 OD单位h⁻¹)、logistic和Gompertz(0.31-0.35 OD单位h⁻¹)以及Richards模型(0.30-0.42 OD单位h⁻¹)。此外,所有模型在较高初始浓度下提供较短的延迟期,如图1(a)所示。初始吸光度(y0)对于所有生长曲线和模型的值在0.071和0.180之间。从初始到最终光密度的吸光度增加(C)对于所有生长曲线和模型的值在0.975和1.107之间。因此,所有模型似乎都表现良好,为这些生长曲线提供了预期的生长参数值。r²值对于所有生长曲线和所有模型均高于0.995,除了三相线性模型,其值低至0.989,因此是数据拟合最差的模型,正如由三条直线组成的模型所预期的那样。所有模型的RMSE值均低于0.035。
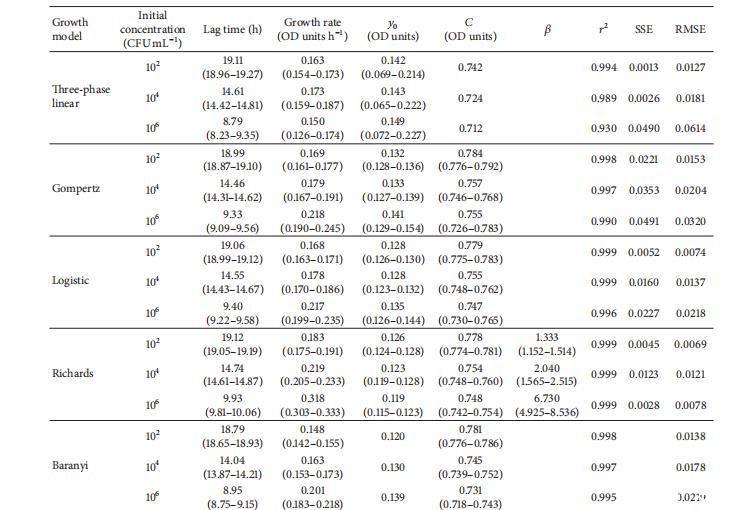
表3显示了五种模型对图1(b)所示单核细胞增生李斯特菌生长曲线提供的生长参数。获得了类似的结果,尽管在这种情况下,唯一对三种测试初始浓度的三个生长率值没有提供显著差异的模型是三相线性。再次,获得了相同的顺序,三相线性模型给出最低值(0.15-0.17 OD单位h⁻¹),其次是Baranyi模型(0.15-0.20 OD单位h⁻¹)、logistic和Gompertz(0.17-0.22 OD单位h⁻¹)以及Richards模型给出最高值(0.18-0.32 OD单位h⁻¹)。此外,所有模型在较高初始浓度下提供较短的延迟期。y0值在0.119和0.149之间,C值在0.712和0.784之间。再次,r²值对于所有生长曲线和所有模型均高于0.990,除了三相线性模型,其值低至0.930。三相线性模型也给出了高达0.061的RMSE值。
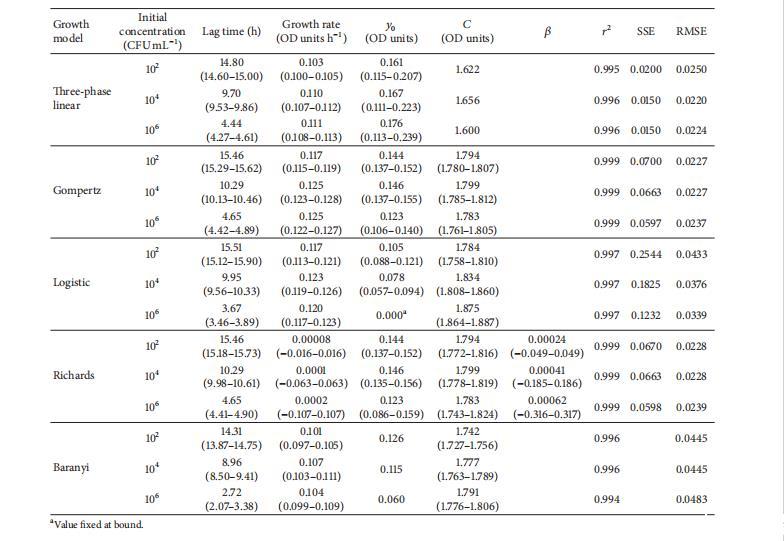
表4显示了五种研究模型对图1(c)所示大肠杆菌生长曲线提供的生长参数。在这种情况下,获得了一些意想不到的结果。三相线性、Gompertz、logistic和Baranyi模型的行为如前所述用于蜡样芽孢杆菌和单核细胞增生李斯特菌。每个模型为三条生长曲线的生长率提供了非常相似的值,它们之间只有轻微差异。然而,只有logistic和Baranyi模型没有提供显著差异。对于这种微生物,再次,三相线性模型给出了生长率的最低值(0.10-0.11 OD单位h⁻¹),但这次与Baranyi模型一起,而logistic和Gompertz模型给出了较高的值(0.12-0.13 OD单位h⁻¹)。然而,Richards模型意外地给出了生长率的低值(<0.001 OD单位h⁻¹)。所有模型在较高初始浓度下提供较短的延迟期。y0值对于所有生长曲线和模型在0.060和0.176之间,除了logistic模型,其对以10⁶CFU mL⁻¹开始的生长曲线给出了异常低的y0值0.000(固定在边界)。Logistic模型对所有三条大肠杆菌生长曲线的SSE值高于0.1,这几乎是表2、3或4中任何其他生长曲线获得值的两倍。在这种情况下,所有生长曲线和所有模型的r²值均高于0.99,包括三相线性模型。
根据图1和表2、3、4所示的结果,研究中选择的生长模型是三相线性、Gompertz和Baranyi。选择的三种模型为生长参数提供了预期值,并正确拟合数据,如分析的统计量所示,即使是三相线性模型,其拟合优度最差,即r²最低和RMSE最高。Richards和logistic模型被disregard,因为它们无法正确拟合所有这些典型生长曲线;即,它们有时给出生长参数的异常值。
每种模型都有提供较高或较低值的趋势,三相线性模型一致给出最低值,其次是Baranyi和Gompertz模型,按此顺序,对于生长率和延迟期。在先前比较这三种模型时,Buchanan等[2]已经注意到并基于每种模型的性质解释了这种效应。这些作者还强调了延迟期持续时间与比生长率值之间存在的相关性。这解释了这些预测模型之间生长率和延迟期值的差异。
因此,似乎取决于选择的预测模型,生长率和延迟时间的值将一致地较高或较低。那么问题是哪种生长模型可以被认为是描述真实种群生长的最佳模型以及为什么。这可以通过对模型的解析方面、机制元素、参数数量、拟合特性等进行深入分析来回答。然而,这样的分析已经在过去进行过[3],但研究人员继续使用和比较不同的生长模型[5,12],可能是因为尚未得出结论性结果。
在这种背景下,我们的观点是,性能最佳的模型是那种对于一种微生物菌株在完全相同的条件下且具有相同预培养历史的不同培养物的生长参数,给出更接近值的模型。
相关新闻推荐
1、肠道菌群是关键:研究揭示茶酚类及其代谢物对细菌生长的差异化影响(一)