2结果与讨论
2.1产絮菌的生长发酵及其絮凝活性
微生物絮凝剂作为产絮菌的发酵代谢产物，其絮凝活性与产絮菌的生长情况有很强的关联性，观测产絮菌J-1在33 h内的生长变化情况，结果见图1。
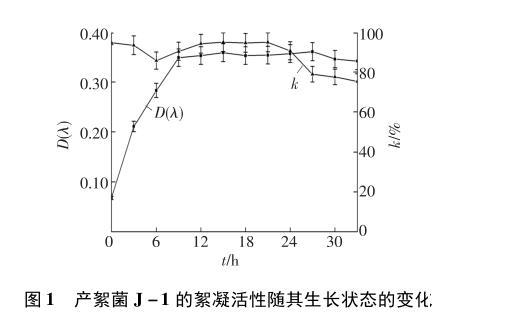
图1产絮菌J-1的絮凝活性随其生长状态的变化
由图1可知，在0～12 h，产絮菌J-1处于对数生长期，理论上，其絮凝率k应随着菌体的快速生长而逐渐升高，但实际却在0～6 h内出现下降现象。这是由于絮凝剂液体培养基造成的误差[8]。空白培养基具有一定的絮凝效果，随着营养成分供菌体生长而消耗，絮凝率呈下降趋势。6 h后随着菌体生长接近最高值，开始不断分泌代谢产物，絮凝率开始上升。12～27 h内，产絮菌J-1处于稳定期，菌体量保持稳定状态，代谢产物大量积累，在15 h时，菌量积累到最大值为2.05 g/L，絮凝率达到94.97%。21 h后产絮菌J-1处于稳定期后期，培养基提供的营养不足以供给菌体生长，代谢产物的分泌呈减缓趋势。27 h后，部分代谢产物被用来弥补培养基营养成分的缺失，产絮菌J-1进入衰亡期，絮凝率继续下降。综上所述，絮凝率的变化趋势符合产絮菌J-1的生长代谢规律。
为进一步验证产絮菌J-1的絮凝活性与其生长代谢规律的关联性，对发酵15 h的产絮菌J-1传代培养10次，观测其菌浊与絮凝率的变化，见图2。
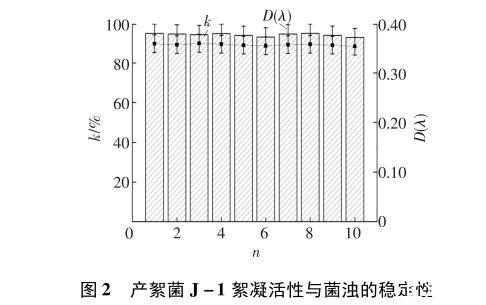
图2产絮菌J-1絮凝活性与菌浊的稳定性
由图2可知，传代次数n为10，产絮菌J-1的絮凝率均保持在95%左右，其菌浊也保持在最高水平。这不仅验证了产絮菌J-1的絮凝活性与其生长代谢规律的关联性，同时证明了产絮菌J-1遗传稳定性优良。
2.2产絮菌的生长动力学模型
为更加科学、客观地掌握产絮菌J-1生长变化的内在规律，观测其33 h内的菌量变化规律，选择Logistic方程建立产絮菌J-1的生长动力学模型。
对Logistic方程积分计算后，得到：
式中：ρ0——初始生物量，g/L，产絮菌J-1的ρ0为0.28 g/L；
ρm——最大生物量，g/L，产絮菌J-1的ρm为2.05 g/L；
K——最大比生长速率，h-1；
t——时间，h；
Y——菌体干重，g/L。
将ρ0和ρm值代入式(1)：
产絮菌J-1的培养时间t为自变量，菌体干重Y为因变量，进行非线性拟合，结果见图3。
由图3可知，Logistic方程基本可以反映产絮菌J-1的生长变化规律。衰亡期菌量的预测值低于实验值，这是由于实验中菌量的测定采取了菌体干重法，既有活菌又有死菌，而Logistic方程对菌量的预测值为活菌量。两者平均残差为0.008，拟合度R2为0.98。利用该拟合曲线，求得K值为0.441，代入式(2)，获得产絮菌J-1的生长动力学模型：
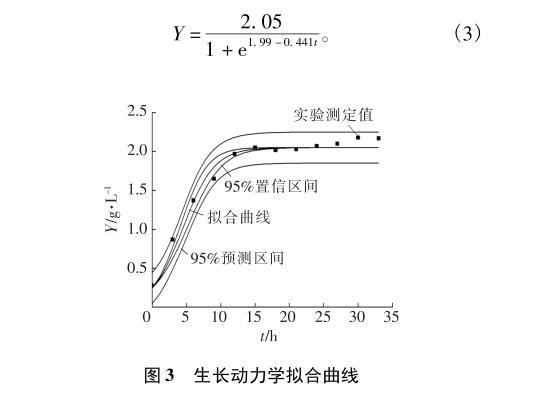
图3生长动力学拟合曲线
产絮菌J-1的比生长速率0.441，高于实验室已有的高效产絮菌的比生长速率0.253，说明产絮菌J-1代时相对较短，为微生物絮凝剂的发酵节约了时间成本。
2.3产絮菌的产物生成动力学模型
图1表明，产絮菌J-1的絮凝活性由其代谢产物确定，且稳定期絮凝率最高，此时菌体生长也达到最高值，比生长速率减缓，菌体生长与产物形成属于部分偶联型，故选取Luedeking-Piret方程进行模拟。
对Luedeking-Piret方程积分计算后，得到：
式中：α——产物生成常数(关联菌体生长)；
β——产物生成常数(关联菌体量);
P——产物生成量，g/L。
代入K值，有
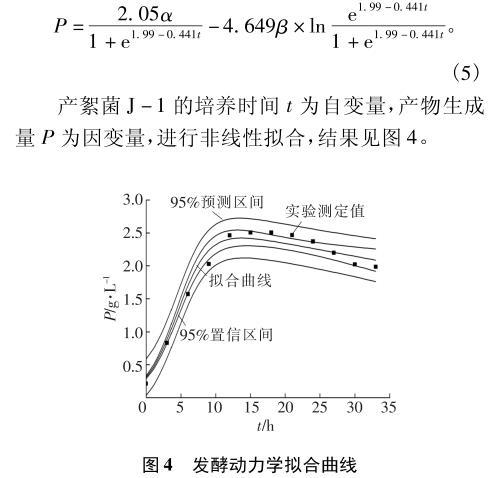
产絮菌J-1的培养时间t为自变量，产物生成量P为因变量，进行非线性拟合，结果见图4。
由图4可知，Luedeking-Piret方程可以较好地反映产絮菌J-1的代谢规律。代谢产物的实验值与预测值的平均残差为0.016，拟合度R2为0.97。利用该拟合曲线，求得α值为1.29，β值为-0.010，代入式(5)，得到产絮菌J-1的产物生成动力学模型：
当α≠0、β=0时，发酵类型属于生长偶联型；α=0、β≠0时，发酵类型属于非生长偶联型；α≠0、β≠0时，发酵类型属于部分生长偶联型。由式(6)可见，当α值越大，β值越小时，产物生成量越高。再次证明了产絮菌J-1发酵微生物絮凝剂的过程为部分偶联型。
综上所述，菌体生长与产物形成属于部分偶联型，所以产絮菌J-1代谢产物的生成与其菌体总量相关，而与菌体生长关联较小。因此，在微生物絮凝剂大量合成前，若比生长速率较大，保证充足的营养和生物量，菌体快速繁殖，菌体总量大量积累，产絮菌J-1代谢产物的合成速率可以得到有效提高。
3结论
(1)产絮菌J-1絮凝活性的变化趋势符合其生长代谢规律。当发酵时间为15 h时，即产絮菌J-1的稳定期，絮凝活性最高为94.97%，且连续传代10次，保持稳定。
(2)利用Logistic方程模拟产絮菌J-1的生长变化规律。实验中菌量测选值与Logistic方程预测值的平均残差为0.008，根据生长动力学拟合曲线，求得K值为0.441，获得产絮菌J-1生长动力学模型。
(3)利用Luedeking-Piret方程可以较好地反映产絮菌J-1的代谢规律。代谢产物实验值与预测值的平均残差为0.016，根据发酵动力学拟合曲线，获得产絮菌J-1的产物生成动力学模型。
相关新闻推荐
2、胰岛素对昆虫病原线虫及其共生细菌伯氏致病杆菌生长、寿命的影响（三）
3、不同浓度冠菌素对番茄防御基因表达、胼胝质沉积及野生型致病菌生长的影响（二）